CodeIQ:共通の祖先は誰だろう
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「共通の祖先は誰だろう」(CodeIQ)を参照してください。
問題の概要
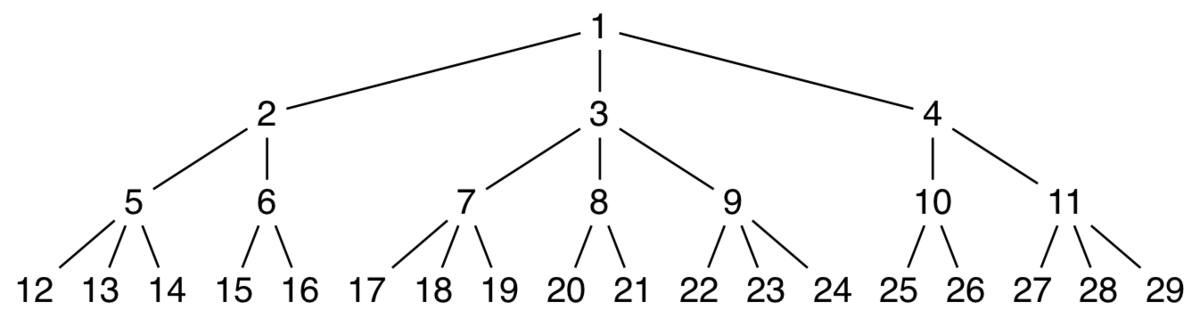
次のような家系図があります。
紙面の都合で 29 までしか書いていませんが、正の整数が全て含まれています。
上が祖先で下が子孫です。
上から順、左から順に 1, 2, ... と番号が振られています。
偶数には子が2人、奇数には子が3人います。 で、複数の数を与えます。共通の祖先の番号のうち、最大のものを出力してください。
【入出力】
入力は
7,20,22
のような感じです。
コンマ区切りで複数の番号が並んでいます。共通の祖先のうち、一番大きな値の番号を計算して、標準出力に出力してください。
出力は、
3
のような感じです。普通に10進数で番号を出力すれば OK です。
ただし、「共通の祖先」に該当する番号がない場合には
-
を出力してください。
末尾の改行はあってもなくても構いません。
(中略)
入力の値は、10億を超えることはありません。
入力の数は、10個を超えることはありません。
「祖先」には自分自身を含みません。[A]と[Aの親]の共通の祖先は[Aの親の親]ということになります。
不正な入力に対処する必要はありません。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
$EndNums = [[1,1]]
# 世代ごとの最初と最後の数字のリストを作る
# (例)
# [1,1]
# [2,4]
# [5,11]
# [12,29]
def makeEndNums()
for parent in $EndNums
first = parent[1] + 1
nums = parent[1] - parent[0] + 1 # 親に含まれる数字の数
odd = 0 # 親に含まれる奇数の数
even = 0 # 親に含まれる偶数の数
if(parent[0]%2 == 0) then # 親の最初が偶数の場合
even = (nums.to_f / 2).ceil
odd = (nums.to_f / 2).floor
else
even = (nums.to_f / 2).floor
odd = (nums.to_f / 2).ceil
end
last = first + 2*even + 3*odd - 1
$EndNums << [first, last]
if last > 1000000000 then break end
end
end
# nの世代を特定する
def searchGeneration(n)
$EndNums.each_with_index{|generation, i|
if generation[0] <= n && n <= generation[1] then
return i
end
}
end
# nの親を返す
def getParent(n)
if n == 1 then return 0 end
g = searchGeneration(n)
first = $EndNums[g][0]
parent_first = $EndNums[g-1][0]
parent_pos = -1
pos = n - first
# まず5で分ける(奇数と偶数が交互に並んでいるので5個ずつ区切ることができる)
div5 = pos/5
mod5 = pos%5
# 親の最初が奇数か偶数かで5で分けた真ん中の値が左右どちらのツリーに含まれるかが決まる
if parent_first%2 == 0 then
# 偶数から始まる場合3個目は右側のツリー
if mod5 < 2 then parent_pos = 2 * div5
else parent_pos = 2 * div5 + 1
end
else
# 奇数から始まる場合3個目は左側のツリー
if mod5 <= 2 then parent_pos = 2 * div5
else parent_pos = 2 * div5 + 1
end
end
return parent_first + parent_pos
end
# nの親のリストを返す
def getParentList(n)
ret = []
begin
n = getParent(n)
if n > 0 then ret << n end
end while n > 0
return ret
end
#main
while line = gets
line.strip!
if line.empty? then next end
inputs = line.split(",").map{|i| i.to_i}
end
makeEndNums()
parent_list = []
for i in inputs
parent_list << getParentList(i)
end
ret = parent_list[0].dup
for i in 1...parent_list.size
ret = ret & parent_list[i]
end
if ret.size == 0 then
puts "-"
else
puts ret.max
end
解説
結構難問と思います。特に最大10億という入力値は相当なもので、数え上げるだけでも制限時間の1秒を超えてしまいます。
基本的な考え方
家系図を作ると制限時間を超えてしまうので、家系図を作らずになんとかしなければなりません。しかし、入力された数値から直接親を計算するのは(できるかもしれませんが)困難です。
まず、入力値に関して知りたいのはそれが何世代目(何段目)にあるのかです。もう一つ、各世代に含まれる数値が幾つから幾つまでなのかが分かれば計算できそうです。
$EndNumsとmakeEndNums()
前述の方針に基づいて家系図の各世代の最初と最後の数値だけを表にします。その表が$EndNumsで、それを構築する関数が$EndNumsとmakeEndNums()です。
ある世代の最初の数と最後の数がわかっているとします。そうすると、次のことがわかります。
次の世代の最初の数はわかっている世代の最後の数+1です。
次の世代にはわかっている世代に含まれる奇数の数×3+偶数の数×2個の数が含まれます。ある世代に含まれる最初の数と最後の数がわかっていればそこに何個の数が含まれるのかがわかり、その最初の数が偶数か奇数かで子供の世代の数の個数を計算できます。
子供の世代の最初の数と個数が分かれば子供の世代の最初の数と最後の数を確定できます。
具体例として図の2世代目[2,4]から3世代目を考えます。
3世代目の最初の数は4+1=5です。
2世代目には3個の数が含まれ最初の数が偶数です。偶数と奇数は順番に並んでいるので2で割れば偶数と奇数の数がわかります。3/2=1余り1で、商の1は偶数と奇数が1個ずつになることは明らかで、最初の数が偶数であることから余りは偶数になります。
なので2世代目には奇数が1つ、偶数が2つあるので3*1+2*2=7が三世代目を構成する数の数になります。
3世代目の最初の数は5なので5から始まって7個目の数は11になります。
よって3世代目は[5,11]になります。
4世代目以降も同じ計算を繰り返せば求めることができます。
makeEndNums()はこれをプログラム化したものです。
入力値の最大が10億なので10億を含む世代に達したら作成をやめます。
getParent()
次の課題は入力値から親の番号を特定することです。
親の世代を知るためには自分が何世代目になるかを求めなければなりませんが、これは$EndNumsから容易にわかります。$EndNumsの各要素の0番目と1番目に間に入力値があればその世代に含まれることになります。これをsearchGeneration()で行います。
入力値の世代がわかったら、入力値が前の世代の何個目の親の木に含まれるかを計算します。例えば3世代目の7は(5,6)、(7,8,9)、(10,11)の3つの木のうちの2つ目に含まれます。2つ目の木に含まれるということは自分の親はひとつ前の世代に含まれる数のうち2番目の値、つまり3であることがわかるというロジックです。
これを計算するためにはまず、入力値がその世代の何番目かを求める必要があります。これは入力値からその世代の最初の数を引けばわかります(54行目)。
この値をposとします。
次に、共通の親を持つ数は「2個、3個、2個、3個、…」か「3個、2個、3個、2個、…」で並んでいます(親の世代が偶数で始まっているか奇数で始まっているかで決まります)。
ということは入力値の世代を5個ずつ区切るとちょうど違う親で区切ることができます。さらに、親の世代が偶数で始まるか奇数で始まるかをチェックすれば5個一区切りの真ん中の値がどちらの親に属するかがわかります。
例えば7の場合、3世代目を5個で区切ると(5,6,7,8,9)と(10,11)になり、親は2から始まるので(5,6,7,8,9)は(5,6)と(7,8,9)に分けることができるので7は2つ目の木に属することがわかります。
コードではこれを計算で求めます。
まず、posを5で割ります。その商(div5)が5個区切りの何番目かを表します(57行目)。
posを5で割った余り(mod5)はposが5個区切りの何番目(0始まり)になるかを表します。例えば7の場合pos=2なのでmod5=2で3番目の値であることがわかります。
親の世代が偶数で始まっている場合、入力値の世代は「2個、3個」の並びなのでmod5が0か1のものが2個のグループ(左側)、2〜4のものが3個のグループ(右側)に含まれます。親の世代が奇数から始まっている場合、入力値の世代は「3個、2個」の並びなのでmod5が0〜2が3個のグループ(左側)、3と4が2個のグループ(右側)に含まれます。
よって、左側グループの場合は2×div5、右側グループの場合は2×div5+1番目の木(=親世代の何番目の数の子)になることを計算できます。
この計算を60〜71行目で行っています。
何番目の親の子かがわかったので親の世代の最初の数から数えて相当する数を返せば親の値になります(73行目)。
getParentList()
結果を求めるために自分の祖先をたどってリストを作る必要があります。
これは自分の番号から親の番号を求め、親の番号からその親の番号、……、と繰り返せばOKです。
この関数ではそれを行います。
getParent()は親がいなかったら0を返す(46行目)ので0が返るまで繰り返し結果を配列に集めて返します。
main
入力値のパースは割愛して、まず全ての入力値に対して親のリストを求めます(97〜100行目)。
次に親の配列の積集合を求めます(102〜105行目)。これが共通の祖先になります。
積集合が空なら共通の祖先がいないので「-」を表示し、そうでなければ積集合の最大値を表示します(107〜111行目)。
雑感
面白い問題でした。
一番悩んだのは56〜71行目の処理です。ブレイクスルーは一旦5個ずつ分割してから再度左右どちらかのツリーに含まれるかを求めれば良いということに気づいたことでした。
この出題者の問題はマップとか表を作って処理するプログラムを書くことが多いような気がします。複数の入力値があってその全てをテストしなければならない問題が多い為、その都度計算するより一旦計算してしまって表引きにするのが効率が良いと思うからでしょう。どうせテストパターンには最大値に近いパターンが含まれるのは確実なので最後まで計算しておいても時間的な損はありませんし。
別の問題の雑感でも書いた気がしますが、一旦計算してしまってその結果を使い回すというのは実際の業務で作るプログラムでも有効な手段です。