CodeIQ:一筆書きの交点
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「一筆書きの交点」(CodeIQ)を参照してください。
問題の概要
一つの円周上で等間隔に並んだ点があります。
任意の点からスタートして、すべての点を通るように直線で一筆書きします。
(すべての点に到達すると、最初の点まで結びます。)
一筆書きする最中に交差する点がいくつあるかを求めます。
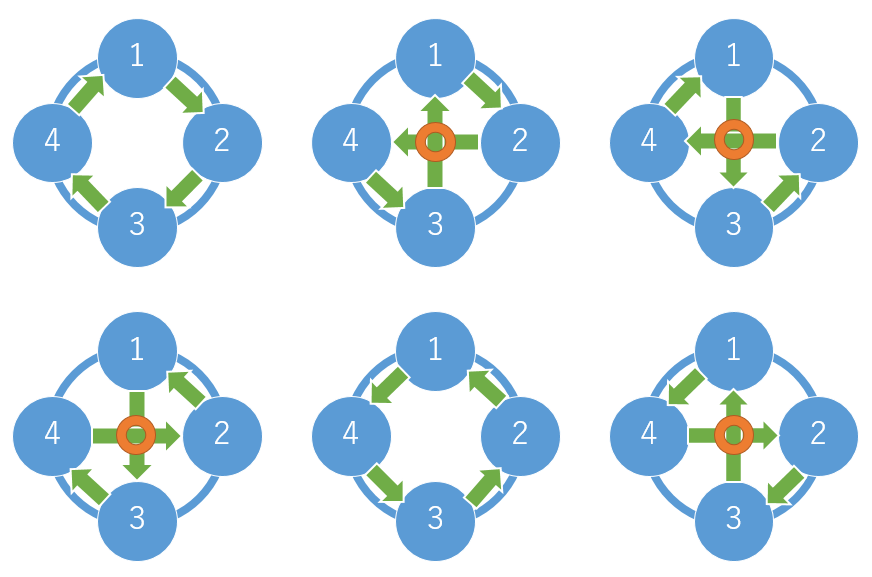
例えば、3点の場合は交差することはありませんが、4点の場合は以下の6通りがあり、丸を付けた4点で交差します。
【問題】
標準入力から n が与えられたとき、n点の間を直線で結んで一筆書きするとき、交差する点の数の合計を求めてください。(nは最大でも9個とします。)
※直線が同じ点で重なる場合も、交差した回数でカウントするため、別々になります。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# 順列
def perm(n,r)
if n == 0 || r == 0 then return 1 end
ret = 1
for i in (n-r+1)..n
ret *= i
end
return ret
end
# 組み合わせ
def cmbin(n,r)
return perm(n,r) / perm(r,r)
end
# 選択した2点を結ぶ線が交わるかどうかをチェックする
def isCrossed(a, b)
a.sort!
b.sort!
# 頂点が同じ場合
if a[0] == b[0] || a[0] == b[1] || a[1] == b[0] || a[1] == b[1] then return 0 end
# (a0, a1)と(b0, b1)があった場合、(a0, a1, b0, b1)か(b0, b1, a0, a1)の順に並ぶ場合は交差しない
if a[1] < b[0] then
return 0
elsif b[1] < a[0] then
return 0
end
# (a0, a1)と(b0, b1)があった場合、(a0, b0, b1, a1)が単純増加・減少している場合は交点ができない
# aとbはソート済みなのでa0とb0を比較して小さい方が外側にあるとみなせる
# 同じ点を含む場合は先に除外しているのでここでは無視できる
if a[0] < b[0] then
if b[1] < a[1] then return 0
else return 1
end
else
if a[1] < b[1] then return 0
else return 1
end
end
end
def countCrossPoint(a, n)
c = [] # 隣合わない2点の配列
for i in 0...(a.length-1)
# 2点の番号の差を求める
d = (a[i+1] - a[i]).abs
# 2点の番号の差が1か全ての点の数-1でない場合(=隣り合う点でない場合)
# その点を結んだ線は点が並ぶ内側で交わるので、点の組を列挙する
if (d != 1) && (d != n-1) then c.push([a[i], a[i+1]]) end
end
# 選んだ2点が交点を持つか調べる
ret = 0
for i in 0...(c.length-1)
for j in (i+1)...c.length
ret += isCrossed(c[i], c[j])
end
end
return ret
end
# main
while line = gets
line.strip!
if line.empty? then next end
n = line.to_i
# 線の結び順を列挙する
ptn = Array((2..n).to_a.permutation(n-1).map{|arr| arr.unshift(1)})
# 数珠順列を考えれば良い(結果は2倍になる)
# 最後の要素を最初の要素と一致させる
ptn = ptn[0...ptn.length/2].map{|arr|
arr.push(1)
}
# 各並びで交差する点の数を数えて合計する
c = 0
for a in ptn
c += countCrossPoint(a, n)
end
p 2*c
end
解説
プログラムで円周上に並んだものを考えるのは結構難しいです。
この問題のポイントは線が交差するというのをどう考えるかでしょう。
main
まず、問題では任意の点から線を引き始めるとなっていますが、初めの点まで戻ってくるので常に1番から始めた場合だけ考えれば十分です。そして、常に1番から始めたとすると一筆書きでたどることのできる順番の組み合わせは円順列になります。
さらに、たどる順番を反転させた場合(例えば、例の図で1→2→3→4→1と1→4→3→2→1、1→2→4→3→1と1→4→3→2、1→3→2→4→1と1→3→4→2→1)は同じパターンだけあるのでたどる順番は数珠順列を考えて結果を2倍すれば同じ値になります。
すると全パターン列挙したとして8!/2=20160通りしかないのでパターンを列挙して総当たりしても時間的に間に合います。
77行目で円順列のパターンを列挙し、81行目でその前半部分だけを集めています。rubyのpermutation()がうまい具合に列挙してくれたので単に前半部分だけを集めれば済みました。81行目のループで末尾に1を加えていますがこれによって[1,2,3,4,1]のようになります。最後の要素が戻ってきた場所の値になるので処理が少し楽になります。
countCrossPoint()は配列要素の順番で番号をたどった時に交差の数を返す関数で、この結果をすべて足し合わせれば答えになります。
countCrossPoint()
引数aは一筆書きでたどる番号の順番、nは点の数(標準入力から取得した値)です。
49行目〜56行目のループで一筆書きでたどる番号のうち(1,2)とか(6,5)のように連続した点以外の組を集めます。2つの番号が連続している場合、そこには交差が発生しないためチェックする必要がありません。
55行目が連続していないことのチェックで2つの番号の差の絶対値が1か(n-1)の場合が連続しないことになります。(n-1)は例の図のようにn=4なら4→1は連続した値とみなす必要があるためです。
そして、集めた点の組みから任意の2つを選択し、isCrossed()でその2つの線が交差するかをチェックします。isCrossed()は交差していれば1、していなければ0を返す関数なので結果を足し合わせれば交点の数になります。
isCrossed()
2つの番号を結ぶ線が交差するかをチェックする関数です。
引数a,bは選択したそれぞれ2点の組みで[1,2]と[3,4]のようになります。
それぞれの点の組を昇順にソートして小さい番号から並べます。2点を結ぶ線が交差するかどうかの判断なので線の向きは関係ありません。あとの処理を楽にするためソートしておきます。
2点のいずれか一方が同じ番号の場合、その番号でつながっているので円の中では交差しません。なので除外します。(24行目)
線が[1,3]と[4,6]や[5,7]と[1,4]の場合、これらは交わりません。a,bはソート済みなのでa[1]<b[0]の場合かb[1]<a[0]の場合にこの条件を満たすことになります。これも除外します。(27〜31行目)
線が[1,6]と[3,5]のような場合もこれらの線は交わりません。a,bはソート済みなのでa[0]とb[0]を比較して小さい方の配列が外側(コメントにあるように[a0,b0,b1,a1]か[b0,a0,a1,b1]のように並ぶ)に来ることが確認できればこれらの線は交わらないので除外できます。
そうではなく、[a0,b0,a1,b1]か[b0,a0,b1,a1]のようになると交わります。
上記のロジックで除外された場合に0を返し、除外されなかった場合は1を返します。
雑感
昔やった「同心円をつなぐ橋」という問題は同心円上の2点を結ぶ線が交差しない場合の組み合わせを求めるという問題だったので、ちょうどこの問題の逆だったのですが、その時は漸化式に基づいて解いてしまったので円周上の2点を結んだ2本の線が交差する場合のアルゴリズムは今回初めて考えました。
プログラムでは円周上であることを簡単に表現するのは難しく、1次元の配列で考えた場合、どのようになるのかという風に問題を捉えなおさなければならないので結構苦労しました。