CodeIQ:永遠に続くビリヤード
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「永遠に続くビリヤード」(CodeIQ)を参照してください。
問題の概要
誰でも楽しめるビリヤード。
今回はクッションに対してちょうど45度の角度にボールを打つことにします。
ボールの勢いが十分に強い場合、クッションに当たると反射し、同じ場所を繰り返して動きます。
簡単にするため、横に m 個、縦に n 個のマス目で任意の格子点から始め、通過したマス目の数をカウントします。
(クッションの角に当たった場合は、来た方向に戻ります。また、同じマスを通過した場合は順方向、逆方向ともに一つとしてカウントします。)
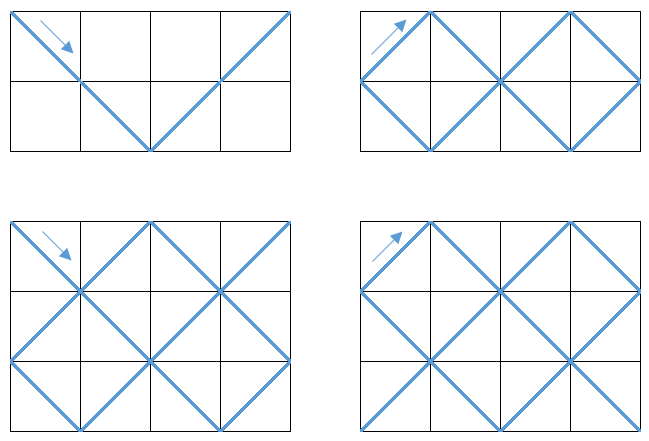
例えば、m = 4, n = 2のとき、左図のように動かすと4マスですが、右図のように動かすと8マスです。
m = 4, n = 3のときはどの位置からどの方向にスタートしても、12マスになります。
標準入力から m と n がコンマ区切りで与えられたとき、通過するマス目の数が最小になる経路、最大になる経路を求め、そのマス目の数をそれぞれ標準出力に出力してください。
(m, n はともに60以下の整数とします。)
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
require 'set'
# 次の位置を返す
# m,n マップのサイズ
# now 現在の位置情報([y,x])
# d 現在の進行方向(Destのどれか)
def move(m, n, now, d)
nxt = [(now[0] + d[0]), (now[1] + d[1])] # 次の位置候補
nd = d.dup # 次の方向
if (nxt[0] < 0) || (m < nxt[0]) then nd = [(-1*nd[0]), nd[1]] end
if (nxt[1] < 0) || (n < nxt[1]) then nd = [nd[0], (-1*nd[1])] end
pos = [(now[0] + nd[0]), (now[1] + nd[1])] # 次の位置決定
return pos, nd
end
# m,n 入力値(マス数)
# st 出発地点を左端の線上に撮った場合のY座標。(Y,0)からスタートするとして扱う
# return 重複のない経路リスト
def countPattern(m,n,st)
now = [st, 0] # 最初の位置はスタート地点
d = [1,1] # 最初の方向は右下に向かう
ret = [] # スタート地点を登録
cnt = 0 # スタート地点に戻ってきた回数
begin
before = now
now, d = move(m, n, now, d)
ret << Set.new([before, now])
# スタート地点に戻ってきた場合のチェック
if now == [st,0] then
cnt += 1
# 次の方向が開始時と同じなら繰り返しなのでやめる
_, nd = move(m, n, now, d)
if nd == [1,1] then break end
end
end while cnt < 2
return ret.uniq.length
end
# 問題を解く
# m,n 入力値(マス数)
# return 最小経路, 最大経路
def solve(m,n)
ret = []
# 2パターンに収束する気がする
for i in 0..1
ret << countPattern(m,n,i)
end
return ret.max, ret.min
end
while line = gets
line.strip!
if line.empty? then
next
end
m,n = line.split(",").map{|a| a.to_i}
mx, mn = solve(m,n)
p mn
p mx
end
解説
この問題は解いてはいますが、これで十分正しいという確証は持っていません。というか「これで多分正しいとは思うけれど、それを数学的にきちんと説明することができない」という状態です。
それでもプログラムの説明をします。
考え方
問題では任意の点から始めるとなっていますが、全ての格子点からのパターンを計算する必要はありません。
例のm=4,n=3のパターンがわかりやすいのですが、このような場合、左右の2パターンで全てのマスの全ての方向(左上と右下を結ぶ場合と右上と左下を結ぶ場合)を通過しています。そして左右の図は上下反転しただけですので、任意の格子点からどの方向に進み始めても最終的には左右の図のどちらかと同じになります。
特殊な場合としてm=4,n=2の角から始めた場合とm=nの場合があります。m=nの場合、角から始めなかった時は長方形を作ってスタート地点に戻ってきます。
ただし、これらの場合でも左辺の格子点の半分(切り上げ)までの点から、右下に向けてスタートした場合だけを考えれば全てのパターンを調べたことになります。
実は経路の長さという観点では(経路の形状は違うけれども)角から始めた場合と左辺の角以外のどこかから始めた場合の2パターンしか考える必要がありません。
countPattern()
この関数が経路の長さを調べる本体です。
nowは現在の位置(格子点を座標として扱った場合の座標)で開始時は左辺の格子点の1つに設定します。
dは現在の向きで最初は右下に向かって進むので[1,1]にします。右上に進む場合は[-1,1]、左下は[1,-1]、左上は[-1,-1]になります。
retは通った経路の集合です。要素にはSet([y1,x1],[y2,y2])を持ち、マスをどの方向(左上<->右下か右上<->左下)かを記録します。Setにしているのは[y1,x1]→[y2,y2]に進んだのか[y2,x2]→[y1,y1]に進んだのかを区別したくないためです。区別しないことによって最後に通過したマスの数を数えるのが楽になります。
cntはスタート地点に戻ってきた回数でループの終了条件になります。スタート地点に2回戻ってきた場合は同じ場所を同じ方向に通っているのでそれ以上やる必要がなくなります。
探索はmove()で1マス進め(31行目)、経路を記録し(32行目)、経路をループし始めたかをチェックし(35〜41行目)、経路をループし始めたらdo-whileループをbreakして、retに記録した経路の長さを返すという流れになります。
35〜41行目の経路をループしているかのチェックは同じマスを同じ方向に通ったかで判定します。
経路の長さはretに記録した座標の重複を除いたretのサイズになります。
move()
1マス移動する処理をします。基本的に現在座標に方向を加えれば良いのですが、辺に達した場合の反射を処理する必要があります。それを行っているのが12〜13行目で、領域外に出てしまったら方向を変えるという処理をしています。
戻り値としては座標と次に進むべき方向を返しますので、countaPttern()ではmove()が返した座標と方向を次のループのmove()の引数にすれば良いことになります。
solve()
この関数は必要なだけスタート地点を設定してcountPattern()を呼び出し、その結果から最小値と最大値を求めるためのものです。
だだし、考え方に書いたように2パターンしか試行していません。きちんと数学的に証明できるわけではないのですが、2パターンで十分なのは次のように理解しています。
基本的にこの問題で求められる経路は一定の長さになるのだと思います。m=4,n=2の左の角から始めた場合、たまたま行きと帰りが全く同じ経路になるためその長さが半分に見えてしまう、ということだと思っています。
例えば格子点に釘が打ってあって格子点を通るように糸を張って行くとします。そうするとm=4,n=2の左の角から始めた場合は行きと帰りで糸が重なってしまうということです。
そして、同じ経路を往復するのは角から始めた場合しかないので左上角とその一つ下の2点だけを調べれば十分ということだと思っています。
雑感
solve()の54行目が1..2になっていますが、ローカルでテストしていた時は1..(m/2.to_f).ceil(つまり、Y方向の格子点の半分切り上げをチェックする)でした(m,nが大きいときに1秒を超えてしまったのでそのままで投稿できませんでしたが)。考え方に書いた通りこれだけのパターンを試せば全ての経路を通っているのでこの結果は100%正しいと自信が持てます。その結果でも経路の長さには2パターンしかなかったので、説明の考えで正しいのだと思っていますが証明できているわけではないので微妙に自信がない部分があります。