CodeIQ：セルの結合で一筆書き

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「セルの結合で一筆書き」（CodeIQ）を参照してください。

問題の概要

Excelのような横にm個、縦にn個のセルがあるとします。このセルを結合して、一筆書きできる図形を作ります。例えば、m=3, n=2のとき、左の図のように結合すると一筆書きできますが、右の図のように結合すると一筆書きできません。
fig1

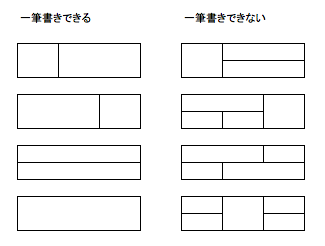
また、下図のような形は一筆書きできますが結合できないので除外します。
fig2

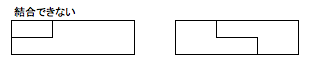
標準入力からmとnがコンマ区切りで与えられます。
結合によって一筆書きできる図形が何通りあるかを出力してください。
結合しなくても一筆書きできる場合、その形も含めるものとします。

私のプログラム

Pythonで解答しています。

#!/usr/local/bin/python3

import fileinput

if __name__ == "__main__":
	for line in fileinput.input():
		line = line.strip()
		if not line:
			continue

		m,n = map(int, line.split(","))
		print((m-1) + (n-1) + 1)

解説

もはやプログラムについて説明することはありません。
入力以外のコードは57行目だけです。
なので考え方だけを説明します。

考え方

一筆書きなので最終的にはオイラーグラフの問題に帰結します。
セルを結合した場合、というより、境界に引いた線をパスとして考えた方がわかりやすいのでそのように考えます。

セルを全て結合した場合の長方形に線を引きます。この線は長方形の外周かすでに引かれた線と交わるまで引いた状態がセルを分割した状態と同じです。そうすると、線を引いた場合、パスの分岐が3（つまりT字）になる場所が（引いた線の数×2）になります。
オイラーグラフと準オイラーグラフが一筆書きできる条件ですが、オイラーグラフではパスの分岐は全て偶数、準オイラーグラフは奇数の分岐は2個です。
つまり、この問題でオイラーグラフになるのは1本も線を引かない場合だけで、準オイラーグラフになるのは1本だけ線を引いた場合です。

で、線を引けるのは結合したセルの境界線なので、この問題で引ける線の数は縦に(m-1)本、横に(n-1)本しかありません。あとは1本も線を引かない場合一通りです。これらを合計すれば答えになります。

雑感

この問題を読んでオイラーグラフの問題ということにはすぐ気付きましたが、問題をやった時点ではオイラーグラフという言葉を知りませんでした。「オイラーが解いたなんとかいう町の橋の問題」というのは知っていたのでWikipediaで調べて知りました。