CodeIQ:コード・トライアスロン2
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「コード・トライアスロン2」(CodeIQ)を参照してください。
問題の概要
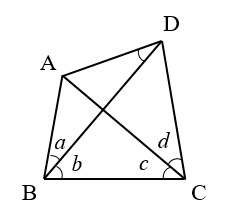
■1■ 四角形ABCDについて、∠ABD=a,∠CBD=b,∠ACB=c,∠ACD=d とおきます。
∠ADB を求めることを考えましょう。
例えば、a=30°,b=50°,c=40°,d=40°のとき、∠ADB=30°となります。
さて、a,b,c,d の値(単位は度)に対し、∠ADB の値(単位は度)を 106 倍したものの整数部分を F(a,b,c,d) と定義します。
例えば、F(30,50,40,40)=30000000 です。
同様に、F(20,60,50,20)=50000000,F(45, 40, 10, 95)=4515341,F(70, 30, 50, 50)=62122012,F(30, 50, 90, 15)=133176131 となることが示せます。
F(a,b,c,d) を求めるプログラムを書いてください。■2■
自然数 n に対し、次の性質をもつ自然数 d の総和を G(n) と定義します。
n を d で割った余りが 1 に等しい。
例えば、G(13)=27 です。13 を 2,3,4,6,12 で割った余りはいずれも 1 だからです。
同様に、G(100)=155,G(102)=101,G(30031)=96767,G(62122012)=101219327 となることが示せます。
G(n) を求めるプログラムを書いてください。
■3■
先頭にゼロを持たない自然数であって、逆から読んでも同じ数になる数を回文数と呼びます。
例えば、1,22,343,440044,7890987 は回文数です。
10,2020,30000,456665 は回文数ではありません。
自然数 m に対し、m 以下の回文数の総和を H(m) と定義します。
例えば、H(20)=56 です。20 以下の自然数では 1~9 と 11 が回文数だからです。
同様に、H(100)=540,H(10000)=545040,H(987789)=533115672,H(101219327)=557319321362 となることが示せます。
H(m) を求めるプログラムを書いてください。■問■
標準入力から、半角空白区切りで自然数 a,b,c,d(a+b+c < 180 かつ b+c+d < 180)が与えられます。
標準出力に H( G( F( a,b,c,d ) ) ) の値を出力してください。
つまり、a,b,c,d の入力に対し、まず F(a,b,c,d) の値(これを P とします)を求めます。
次に P に対し、G(P) の値(これを Q とします)を求めます。
最後に Q に対し、H(Q) の値(これを R とします)を求めます。
標準出力に R の値を出力してください。(P, Q の値は出力しないでください。)
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
require 'prime'
#==============================================================================
# ■ 1 ■
#==============================================================================
def toRad(x)
return x * Math::PI / 180.0
end
def toDeg(x)
return x * 180.0 / Math::PI
end
def sinD(x)
return Math.sin(toRad(x))
end
def cosD(x)
return Math.cos(toRad(x))
end
def atanD(x)
return toDeg(Math.atan(x))
end
# ラングレーの問題
# 参考:http://d.hatena.ne.jp/rsc96074/20121016/1350347823
def F(a, b, c, d)
n = b+c
e = 180 - (n+d)
f = 180 - (a+n)
m = (sinD(b)*sinD(d)*sinD(f))/(sinD(a)*sinD(c)*sinD(e))
if e <= 0 || f <= 0 then return -1.0 end
for x in 1...n
if sinD(n-x)/sinD(x) == m then return x*1000000 end
end
x = atanD(sinD(n)/(cosD(n)+m))
x = x >= 0 ? x : 180 + x
return (x.round(8) * 1000000).floor
end
#==============================================================================
# ■ 2 ■
#==============================================================================
def devSumSub(arr)
s = 0
for i in 0..arr[1]
s += arr[0] ** i
end
return s
end
def divSum(fs)
s = 1
for arr in fs
s *= devSumSub(arr)
end
return s
end
# 参考:http://mathtrain.jp/yakusuwa
def G(n)
fs = (n-1).prime_division
return divSum(fs) - 1
end
#==============================================================================
# ■ 3 ■
#==============================================================================
Kaibunsu = [
[0,1,2,3,4,5,6,7,8,9],
[00,11,22,33,44,55,66,77,88,99],
]
def makeKaibunsu(n, r)
if r == 0 then
return Kaibunsu[r][0..n].reduce(:+)
elsif r == 1 then
return Kaibunsu[r][0..(n/11)].reduce(:+)
end
base = 10**r + 1 # 作成する桁数の回文数の基本値(5けたなら10001)
Kaibunsu.push([])
sum = 0
for m in 1..9
# 作成する回文数の間の値のKaibunsuの添え字の開始番号を決定する
# 5けたなら(1..9)、(101..999)が間に入る
l = r % 2
while l < r
for a in Kaibunsu[l]
x = m*base + a*(10 ** ((r-l)/2))
if x > n then
return sum
else
Kaibunsu[r].push(x)
sum += x
end
end
# 次のKaibunsuの添え字
# 奇数桁の回文数を作る場合は奇数桁の値だけ、偶数桁の場合は偶数桁の値だけが間に入る
l += 2
end
end
return sum
end
# n以下の回文数を求める
def H(n)
r = Math.log10(n).floor
s = 0
for i in 0..r
s += makeKaibunsu(n,i)
end
return s
end
#==============================================================================
# main
#==============================================================================
while line = gets
line.strip!
if line.empty? then next end
a,b,c,d = line.split(" ").map {|n| n.to_i}
p H(G(F(a,b,c,d)))
end
解説
ヘビーな問題です。単純にやったら1つだけでも時間切れになりそうな問題が3問の上、それぞれの問題がそこそこ難しいです。
■1■ - ラングレーの問題
最初、私はこの問題は「ヨユー」と思いました。一見中学校レベルの数学の問題に思えたからです。手計算で一般解を求める式にしてしまえばO(1)で解けるようにできると思いました。しかし、1時間ほど頑張りましたが分からない(T^T)。確かに高校レベルの数学はかなり忘れました。しかし、中学校レベルならいけるはずです。三角形ABCも三角形DBCも一意に定まります。なので四角形ABCDも一意に定まります。なのに解けない……。仕方ないのでGoogle先生に聞いたらこれは「ラングレーの問題」という難問であることがわかりました。解けないはずです。
仕方ないので一般解を調べました。で、見つけたのが参考のURLです。私の解答は基本的に参考URLのコードをRubyに移植しただけです。atan()とか出てきています。私には解説できませんので参考URLを見てください。
さて、これで一番気になるのが浮動小数点誤差です。実際、問題の例としてあげられていたパターン(未引用)のうち1つは浮動小数点誤差によって正しい値になりませんでした。そこで43行目では問題に合わせて1000000倍すると共に小数点以下2けた目を丸めています。
■2■ - 約数の総和
この問題も自分で考えていません。
約数を高速に求める方法を探していたら、約数の総和を求める記事が見つかったためその方法の通りに実装しました。Rubyの場合、約数はprime_division()で求められることがわかったのでそれを利用しました。
この問題については説明できます。
具体的な例として参考URLと同じく12の場合を考えます。12の約数は1、2、3、4、6、12です。これは1、2、3、22、2×3、22×3です。つまり、[2,2,3]のうち2の0〜2乗、3の0〜1乗で作られるすべての数の総和ということです。
これを一般化すると参考のURLの形になります。
ただし、問題はnを割ったあまりが1に等しい数なので、(n-1)の約数のうち1以外のものがnを割ったらあまりが1になる数になります。
■3■ - 回文数
この問題も調べて済まそうと思いましたが、回文数を作るアルゴリズムを見つけられなかったので自分で作りました。
makeKaibun(n, r)が回文数を作る関数でnはこれより大きい値にはしないという指定、rは作成する桁数-1です。そして、この関数はより小さい桁数の回文数が作成済みでなければなりません。
なのでH(n)ではr=0からnの桁まで順に回文数を作成しています。
考え方はこうです。
例えば5桁の回文数を作る場合、10001〜90009の0の部分を3桁、および1桁の回文数で埋めれば良いわけです。3桁の回文数で埋めれば11011〜99999ができ、1桁の回文数で埋めれば10001〜90909ができます。さらに3桁の回文数は101〜909の0の部分を1桁の回文数で埋めればできるので動的計画法が使えます。
もう一つ考えておかなければならないのは桁数が奇数と偶数で場合分けが必要と追いことです。例えば1001〜9009の0の部分は00〜99で埋めないと回文数になりません。
プログラムでは1桁の場合と2けたの場合は初期値として定数化しています。ここに0を含めるのがちょっとしたポイントでこれがないとうまく回文数を作れません。
94業目のlは桁数が奇数か偶数かを判断します(実際には桁数が奇数の場合が0、偶数の場合が1になります)。これによって回文数の初期値に0〜9を使うか00〜99を使うかが決まるのであとはlを2ずつ増やせば間に入れる数をうまく選ぶことができます。
98行目の「a*(10 ** ((r-l)/2))」ですがaはKaibunsuから選んだ間に入れる数です。(10 ** ((r-l)/2))は選んだ数を間に入れるために何桁左にずらせば良いかを計算しています。例えば5けたの10001に101を入れる場合10倍しなければなりません。3を入れる場合は100倍しなければなりません。この計算をしています。
それからnよりも大きな数は作る必要がないのでチェックして終了します(101行目)。
後は作成した回文数を順次足しておけば答えになります。
雑感
この問題は■1■でつまずきました。その上、浮動小数点誤差周りが怪しいという。うまく整数だけを使って解くことができるのでしょうか?