CodeIQ：共通の友達の最大数は？

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「共通の友達の最大数は？」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

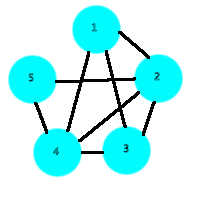
例えば、次の図のような友人関係の場合、共通の友達の最大数は3人になります。
（2番の人の友人が1, 3, 4, 5で、4番の人の友人が1, 2, 3, 5のため）


標準入力から次のような入力があります。
【入出力サンプル】
INPUT
5
1 2
1 3
1 4
3 4
2 3
2 4
2 5
4 5
OUTPUT
3
1行目がこのリストに登場する友人番号の最大値、2行目以降に友人関係がある場合に、そのペアを空白区切りでセットされています。
このとき、標準出力に「共通の友達」の最大値を出力します。

私のプログラム

Javaで解答しています。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
 
/**
 *
 * @author kamio
 */
public class Main {
 
    // 1人の友人を管理するクラス
    public class Person {
        long[]  Friends;            // 友達の場所（0始まりなので-1）のビットに1を立てる。
        private final int Max;      // メンバの数
        int ID = 0;                 // 自分のID
        int FriendsNum = 0;         // 自分の友人数
 
        /**
         * コンストラクタ
         * @param n 友人の最大数
         * @param id 自分のID（0始まり）
         */
        public Person(int n, int id){
            Max = n;        // 友人の数（自分を含む）
            ID = id;        // 自分のIDをセット
            int size;   // 必要なビット数分配列を用意する
 
            if(n%64 == 0){
                size = n/64;
            } else {
                size = n/64 + 1;
            }
 
            Friends = new long[size];
        }
 
        /**
         * 友達の場所に1を立てる
         * @param pos 友人のID（1始まり）
         */
        public void set(int pos){
            int row = (pos-1)/64;    // 配列の何個めを使うか
            int col = (pos-1)%64;  // 使用する配列要素の何ビット目か
 
            Friends[row] |= 0x8000000000000000L >>> col;
        }
 
        /**
         * 友人の一覧を表示する
         * @param f 友人のリスト
         */
        public void printFriends(long[] f){
            for(int j=0; j<f.length; j++){
                long l = f[j];
 
                for(int i=0; <<64; i++){
                    if(((l<<i) & 0x8000000000000000L) != 0){
                        System.out.print((j*64+i+1) + " ");
                    }
                }
            }
            System.out.println("");
        }
 
        /**
         * 自分の友人の番号を列挙する（デバッグ）
         */
        public void printFriends(){
            System.out.print((ID+1) + ": ");
            printFriends(Friends);
        }
 
        /**
         * 引数の友人と共通の友人を返す
         * @param p 友人のID
         * @return 共通の友人リスト
         */
        public long[] getCap(Person p){
            long[] ret = new long[Friends.length];
 
            for(int i=0; i<ret.length; i++){
                ret[i] = Friends[i] & p.Friends[i];
            }
 
            return ret;
        }
 
        /**
         * 1が立っているビットを返す
         * @param v ビットを数えたい値
         * @return 1が立っているビットの数
         */
        private int count64bit(long v){
            long count = (v & 0x5555555555555555L) + ((v >> 1) & 0x5555555555555555L);
            count = (count & 0x3333333333333333L) + ((count >> 2) & 0x3333333333333333L);
            count = (count & 0x0f0f0f0f0f0f0f0fL) + ((count >> 4) & 0x0f0f0f0f0f0f0f0fL);
            count = (count & 0x00ff00ff00ff00ffL) + ((count >> 8) & 0x00ff00ff00ff00ffL);
            count = (count & 0x0000ffff0000ffffL) + ((count >> 16) & 0x0000ffff0000ffffL);
            return (int)((count & 0x00000000ffffffffL) + ((count >> 32) & 0x00000000ffffffffL));
        }
 
        /**
         * 友達の数を返す
         * 自分以外の友人数（共通の友人数など）を数えるため引数をとる
         * @param v 友人リスト
         * @return 友人の数
         */
        public int countFriendsNum(long[] v){
            int count = 0;
            for(int i=0; i<v.length; i++){
                count += count64bit(v[i]);
            }
            return count;
        }
 
        /**
         * 自分の友人数を計算する
         */
        public void calcFriendsNum(){
            FriendsNum = countFriendsNum(Friends);
        }
    }
 
    /**
     * グループ（Personの集まり）
     */
    ArrayList<Person> Group;
 
    /**
     * コンストラクタ
     */
    public Main(){
        Group = new ArrayList<>();
    }
 
    /**
     * グループのメンバでグループを初期化する
     * @param n メンバ内の人数
     */
    public void init(int n){
        for(int i=0; iGlt;n; i++){
            Group.add(new Person(n, i));
        }
    }
 
    /**
     * 友人をそれぞれに設定する（1始まり）
     * @param p1 友人関係にある一方のメンバのID
     * @param p2 友人関係にある他方のメンバのID
     */
    public void set(int p1, int p2){
        // Groupのインデックスは0始まり。setは1始まり。
        Group.get(p1-1).set(p2);
        Group.get(p2-1).set(p1);
    }
 
    /**
     * 入力が終わった時点で友人の数をカウントする
     */
    public void calcFriendsNum(){
        for(Person p: Group){
            p.calcFriendsNum();
        }
    }
 
    /**
     * 友人の一覧を出力する（デバッグ）
     */
    public void printFriends(){
        for(Person p: Group){
            p.printFriends();
        }
    }
 
    /**
     * 共通の友人の最大数を返す
     * @return 共通の友人の最大数
     */
    public int getMaxCommon(){
        int max = 0;
        for(int i=0; i<Group.size(); i++){
            Person p1 = Group.get(i);
 
            for(int j=i+1; j<Group.size(); j++){
                Person p2 = Group.get(j);
 
                // 友人数が現在の最大値より小さい場合は無視して良い
                if(p2.FriendsNum < max){
                    continue;
                }
                else{
                    long[] c = p1.getCap(p2);
                    int n = p1.countFriendsNum(c);
                    if(n>max){
                        max = n;
                    }
                }
            }
        }
        return max;
    }
 
    /**
     * @param args the command line arguments
     * @throws java.io.IOException
     */
    public static void main(String[] args) throws IOException {
        try (BufferedReader stdReader = new BufferedReader(new InputStreamReader(System.in))) {
            Main MxC = new Main();
            String line;
            int lcount = 0;
            while ((line = stdReader.readLine()) != null) {
                line = line.trim();
                if(line.isEmpty()){
                    break;
                }
 
                if(lcount == 0){
                    int n = Integer.parseInt(line);
                    MxC.init(n);
                    lcount++;
                    continue;
                }
 
                String[] splited = line.split(" ");
                int p1 = Integer.parseInt(splited[0]);
                int p2 = Integer.parseInt(splited[1]);
 
                MxC.set(p1, p2);
                lcount++;
            }
 
            MxC.calcFriendsNum();
 
            int max = MxC.getMaxCommon();
            System.out.print(max);
        }
    }
 
}

解説

CodeIQの回答のコードとしてはかなり長いコードです。デバッグプリントを含んでいるのもありますが、入力される人の数が64bit整数の範囲に収まるかどうかが問題になかったのでそれに対応するために長くなった部分もあります。
ちなみに、これは★★★で難しいとされている問題です。

基本方針

実のところ、基本的なロジックは単純です。
各人にそれぞれの友人集合を持たせ、2人を選んでその共通部分が最も多い数を出力すれば良いだけです。問題はこれをいかに高速化するかと言う部分にあります。

Personクラス

普通に考えると友人のリストをSet<int>にするとことでしょうが、計算速度が気になります。そこで私は友人かどうかを表すためにビットフラグを使用しました。各人にはIDが振られているのでそのビットが1であれば友人、0なら友人でないとします。このようにすると2人の共通の友人を求めるのに論理積を取れば良いだけなので非常に高速に計算できます。

ただし、問題はlongでも63人（自分を除くため）までしか管理できません。微妙な数字なので配列にして任意の人数を管理できるようにしました。それがPersonクラスのFriendsです。

Personクラスは他にもメンバ変数を持っていますが、重要な変数はID（自分の番号）で、その他は処理を楽にするためのものです。

メソッドには次のものがあります。デバッグ用のメソッドは説明を省きます。
メソッド 説明
set() 友人をFriendsに設定します。
64人を超えた場合にFriendsのどの要素を使うべきか決定するための処理をしていますが、指定の位置にビットを立てるだけです。これを考えていた時、頭の中のイメージで左側から1,2,3,…とイメージしていたままビットを立てていますが、普通に最下位ビットから使えば問題ありませんでした。
getCap() 自身と引数に与えられた人の共通の友人の集合を返します。
双方のFriendsの論理積をとり、その配列を返します。
count64bit() longの値の1が立っているビットの数を返します。
countFriends() count64bit()をFriendsに適用して友人の数の合計を返します。
calcFriendsNum() 自分の友人数を返すcountFriends()のラッパ関数です。

Mainクラス

MainクラスのGroupメンバ変数はPersonのリストで、入力値を管理します。
init()でGroupを初期化し、set()で標準入力から得た友人情報を設定します。
calcFriendsNum()はgetMaxCommon()の処理を高速化するため、各人の友人数を計算しています。
まず、main()では入力値に対してこれらのメソッドを使ってデータをセットします。

データをセットし終わったらgetMaxComon()で共通の友人数の最大値を求めます。
基本的に総当たりで計算しているだけですが、高速化のため若干の工夫をしています。それはあるIDの友人数が現在の共通の友人数の最大値より少なければ最大値を更新することがないので無視して良いということです。もし、時間切れでリジェクトされたら更に友人数で降順にソートしてから処理するつもりでしたがその必要はありませんでした。
共通の友人数を求める処理はPerson::countFriendsNum()でやっています。これは先に説明した通りです。

雑感

プログラムが長い割にそれほど難しいことはしていません。
この問題をやった時点ではまだPythonを覚えていなかったのですが、Pythonの様に自動的に任意精度整数を使える言語なら人数が64人を超えても気にしなくて良いので、ずっとプログラムが短くなります。わざわざクラスを作る必要もなく、整数の配列を用意するだけで事足りてしまいます。

私は、この問題は仕事で使うプログラムでも似た様なことをする場合がありそうな良い問題だな、と思った記憶があります。