CodeIQ：三角形に分割しよう

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「三角形に分割しよう」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
（三次元のグラフィックにおいて、立体的な形状を、メッシュと呼ばれる多数の三角形で表現します。
ここでは平面に与えられる多角形を対角線で分割して、三角形を組み合わせて表現されるようにします。
このとき、切断する対角線の長さの和が最小になるような切り方を求め、その対角線の長さの和を求めてください。
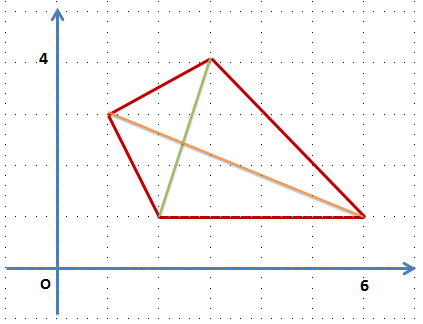
下図のような場合、緑の対角線とオレンジの対角線が考えられますが、緑の方が短いので、この長さが最小になります。
fig.1

各頂点の座標は整数で与えられるものとし、最大10個が入力されます。
答えは小数第三位を四捨五入して小数第二位まで求めてください。
（ヒント：対角線の長さは三平方の定理で求めることができます。）

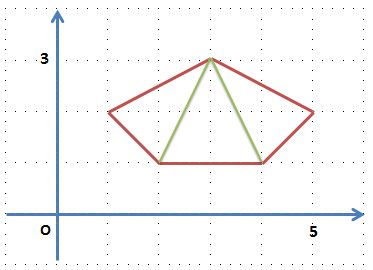
例えば、以下の入力が与えられる下図のような五角形の場合、
図にある緑の対角線の長さを合計して、答えは「4.47」となります。
（与えられた順に線をつなぎ、最後の点と最初の点をつなぐものとします）

【入力】
1,2
2,1
4,1
5,2
3,3

fig.1

なお、今回は凸多角形のみ対象とし、切断する対角線は頂点以外の場所で交差しないものとします。

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

$Min = Float::INFINITY

def solve(points, arr, sum)
	# 3点になったら対角線は引けないので終わり
	if arr.size == 3 then
		$Min = sum if sum < $Min
		return
	end

	for i in 0...arr.size
		n = arr[i]	# 任意の点を選択
		j = i + 2	# 1個とばした点のインデックスを対角として選択
		j -= arr.size if j >= arr.size	# 範囲外の調整
		m = arr[j]	# 対角

		# 対角線の長さを計算
		v = Math.sqrt((points[m][0] - points[n][0])**2 + (points[m][1] - points[n][1])**2)

		d = i + 1	# とばした点のインデックス
		d -= arr.size if d >= arr.size # 範囲外の調整

		nxt = arr.dup
		nxt.delete_at(d)	# とばした点を削除

		solve(points, nxt, sum + v)
	end
end

# main
points = []
while line = gets
	line.strip!
	next if line.empty?

	pt = line.split(',').map{|v| v.to_i}
	points << pt
end

arr = (0...points.size).to_a
solve(points, arr, 0.0)

p $Min.round(2)

解説

★★の問題としてはやや難しいかなぁ、と思います。

考え方

対角線の長さを求めるのはヒントにある通り三平方の定理で簡単に求められますから問題ではありません。
問題は対角線の引き方です。Wikipediaのページを参照してください。これの7各系の42通りの分割のようなパターンを列挙して、それぞれの対角線の長さを列挙する必要があります。

この方法ですが、次のようにしてできます。
任意の頂点を1つ選びます。
その頂点の右隣を1つ跳ばした頂点を対角線を引く場所として選択します。
先ほど跳ばした頂点を削除します。
こうして1つ頂点が減った多角形に対してこの操作を繰り返します。
三角形になったら終わりです。

このようにして対角線を決めながらその合計を求めて行き、最小のものを探します。

main

入力値を読み取って頂点のリストpointsを作ります。
また、考え方に書いた通り対角線を引いて頂点を除いてゆくので、残っている頂点を管理するためarrを作成します。arrには残っている頂点のインデックス番号が入っています。
solve()に頂点の座標リスト、残りの頂点リスト、対角線の長さの合計を渡し、最小値を求めます。
$Minに最小値が記録されるのでそれを小数点以下2桁に丸めて表示します。

solve(points, arr, sum)

考え方に書いた通り対角線を引きながら頂点を減らして行き、同時に対角線の長さの合計を求めます。
引数pointsは頂点の座標リスト、arrは残りの頂点リスト、sumは対角線の長さの合計です。

まず、頂点の数が3になったらそれ以上対角線を引けないので終わりです。
$Minとその時のsumを比較してsumの方が小さければ$Minを更新し、リターンします。

arrから任意の頂点を選びます。
そこから1つ頂点を跳ばして対角線を引く位置を決定します。
（最後の頂点になったら最初に戻るようにしていますが、不要だった気がします）

対角線の長さを三平方の定理に従って計算します。

nxtにarrをコピーし、跳ばした頂点のインデックス番号をnxtから削除します。

この結果を使ってsolve()を再帰的に呼び出します。

雑感

最初やった時、対角線はWikipediaのページの図の1行目の5個目、3行目の2個目、3行目の4個目のようなパターンしかないと思っていて、間違えました。
後、「与えられた順に線をつなぎ、最後の点と最初の点をつなぐものとします」と書いてあるので頂点は入力順に繋げば良いということだと思うのですが、ちょっとわかりにくい。
問題を読んだ時に、順番に繋いだら多角形にならない場合はどうするんだろうと結構悩みました。結局、順番に繋いでダメならその時考えようということで無視しましたが。