プログラム解説：CodeIQ「壊れたパスカルの三角形」

問題の概要

問題を引用します。

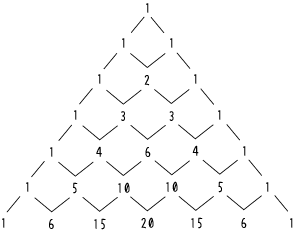
【パスカルの三角形】

パスカルの三角形は、上記のように隣り合った数の和を下段に書くことで作ることができます。

【問題】
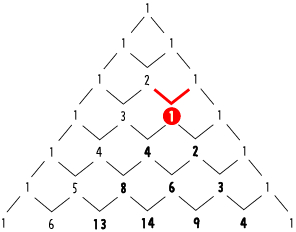
パスカルの三角形を作るとき、隣り合った数の和を下段に追加していきますが、一か所だけ差を計算してしまっています。
次の図では、4段目・左から3つ目の値が、2 - 1 = 1になっているので、そこから下の部分の数が通常のパスカルの三角形と異なっています。

このような、壊れてしまったパスカルの三角形の一番下の段が入力として与えられたとき、“何段目の”、“左から何番目”の値を求める際に差を計算してしまったのかを特定するプログラムを書いてください。
※「差」は、『大きい方の値から小さい方の値を引く』と考えてください。

【入力】
入力データは1行目にパスカルの三角形の段数k、2行目にk個の整数値が半角スペース区切りで与えられます。
kは最大60です。
k個の整数値は、壊れたパスカルの三角形のk段目を表しています。
これらの値を読み込み、間違えた計算方法で計算してしまった部分（差を計算した部分）を特定し、その段数と左から数えて何番目に当たるかを半角スペース区切りで出力してください。

（例）
※上記の問題文の図を使った例になります。
<入力>

7
1 6 13 14 9 4 1

<出力>

4 3

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

def getBefore(arr)
	ret = [1]

	for i in 1...(arr.size-1)
		ret << arr[i] - ret[i-1]
	end

	return ret
end

def combin(n, r)
	ret = 1

	n.downto(n-r+1){|i| ret *= i }
	r.downto(2){|i| ret /= i }

	return ret
end

def check(n, arr)
	cor = []
	for i in 0..(n-1)
		cor << combin(n-1, i)
	end
#	printf("cor: %s\n", cor.to_s)

	dps = []
	for i in 0...arr.size
		dps << i if arr[i] != cor[i]
	end

	return dps[0] if dps.size == 1
	return -1
end

def solve(n, arr)
	now = arr

	(n-1).downto(1){|i|
		nxt = getBefore(now)
#		printf("nxt: %s\n", nxt.to_s)
		d = check(i, nxt)
		if d != -1 then
			return [i, d+1]
		end

		now = nxt
	}
end

# main
l = 0
n = 0
arr = nil

while line = gets
	line.strip!
	next if line.empty?

	if l == 0 then n = line.to_i
	elsif l == 1 then arr = line.split.map{|v| v.to_i}
	end

	l += 1
end

puts solve(n, arr).join(" ")

解説

私のプログラムは正しく答えを求められますし、効率も悪くないと思いますがもっとうまい方法がありそうに思えます。

考え方

パスカルの三角形のk段目の数字は二項定理で簡単に求められます。

また、入力値からk-1段目は次の様にして求められます。
例を使って具体的にやります。

入力値：（7段目）1 6 13 14 9 4 1

格段の左端は1と決まっているので、k段目の1個目（0始まり）から1を引きます。
　6-1 = 5
これがk-1段目の1個目の値になります。
なのでこの時点でk-1段目は[1,5]が確定します。
同様にk段目の2個目からk-1段目の1個目の値を引きます。
　13-5=8
これがk-1段目の2個目の値です。
　[1,5,8]
同様に繰り返してk-1段目を確定できます。
k-2段目以降も同様にして求められます。

最初に間違った場所は二項定理で求めた値と前述の様に計算した値を比較して異なる場所が初めて1個になった場所です。

main

入力値kを数値、k段目の値を数値の配列にしてsolve()に渡します。
戻り値を印字します。

solve(n, arr)

引数nはn段目、arrはn段目の値です。
n-1段目から上に向かってgetBefore()で値を確定します。
check()で二項定理で求めた正しい値と比較します。
checkは2箇所以上違っている場合は-1、1箇所だけ違った場合はその場所（0始まり）を返すので[i, d+1]（dはcheck()の戻り値）が答えになりますからそれを返却します。

check(n, arr)

引数nはn段目、arrはn段目の値です。
まず、配列corに二項定理で正しいn段目の値を求めます。
arrとcorを比較し、異なる値の位置をdpsに保持します。
dpsの要素数が1ならそこが初めて間違った場所なのでそれを返します。
そうで無ければ-1を返します。
答えでない場合-1を返すのは位置が0以上なので、位置として取り得ない値だからです。

combin(n,r)

_nC_rを返します。

getBefore(arr)

考え方に書いた通りに引数arrからその前の段の値を求めて返します。

雑感

なんとなく二項定理で求めた値と比較ではなく、格段の値だけから答えを求める方法がありそうに思えます。

CodeIQ：壊れたパスカルの三角形